研究报告:永续时间转换期权的定价方式
要闻速递作者:DeFi研究员 Vincent Lu
Pechtl的模型
1995年,Pechtl提出离散时间转换认购期权,如果在Δt内,资产价格超过了行权价X,则投资者可以在期权到期的时候获得这段时间的收益为AΔt(A为某个常数),同理,在离散时间认沽期权中,在某个Δt内,资产价格低于了行权价X,则投资者可以在期权到期的时候获得这段时间的收益为也为AΔt。
Pechtl根据理论和BS模型,他计算出这种认购期权的定价可以用如下算式来表达:
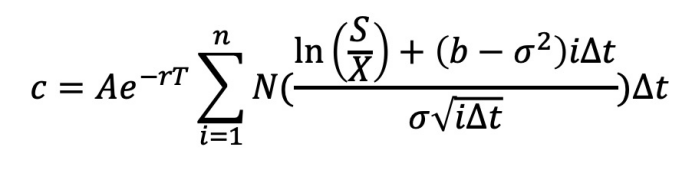
认沽期权的定价可以用如下算式来表达:
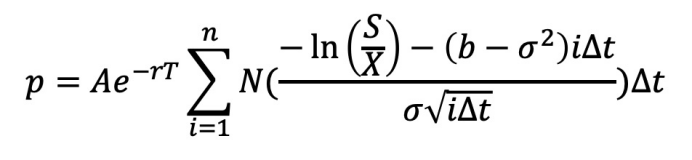
其中S为现价,X为行权价,波动率为σ
在这两个算式中,n = T/Δt,如果期权合约已经生效了一段时间,则需要在期权定价公式中增加一项:ΔtA·exp(-rT)·m,其中m是已经满足时间转换条件的时间单位数量(例如,认购期权已经生效了20天,其中10天价格超过了行权价格)
基于Pechtl模型的改动
我们对Pechtl的理论做一点小改动,如果某投资者能在认购期权价格超过行权价格的时候就获得收益,并且收益的计算方式为(当前价格-行权价格)*Δt,例如,Alice从Bob那里买了一个行权价格为110美元的认购期权,到期时间是1年。在这年里,价格在11月份突破了行权价,到达了120~130美元,而到了十二月份,价格下跌,跌破了90美元,虽然到期时间来临时,期权价格仍然低于110美元,但是Alice仍然可以在11月获得期权高于行权价的那部分收入。
考虑到在Pechtl模型中,收益为到期日后才获得,所以在估算价格中,会有折现因子exp(-rT),其中r为无风险利率。那如果当时就行权,在第i个周期内,获得概率的可能性应为:
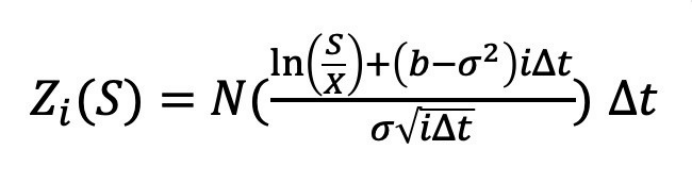
我们的认购期权模型中,另一个改动是超过行权价,投资者获得的收益为(当前价格-行权价格)??Δt,而不是像Pechtl模型中的固定常数A,在这种情况下,我们必须修订Pechtl的公式,应该用每个(当时价格-行权价格)??(这个价格出现的概率)并累加。在数学上就是积分的形式(因为Z表示概率累积,因此某个价格出现的概率应为Z关于价格的一阶导数):
模型中的另外一个改动就是:购买认购期权的投资者是立即获得收益,而不是等到到期日之后才会获得,因此需要把每天的收益折现到当前。考虑到无风险利率是r,那么每天的收益即为r/365,第i天的现值(PV)应该为:
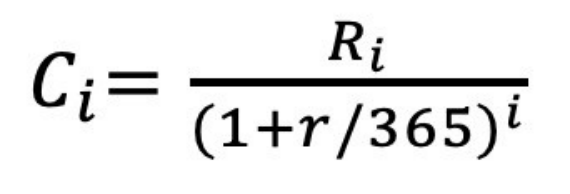
把所有的Ci累加,就得到了这种期权的定价方式:
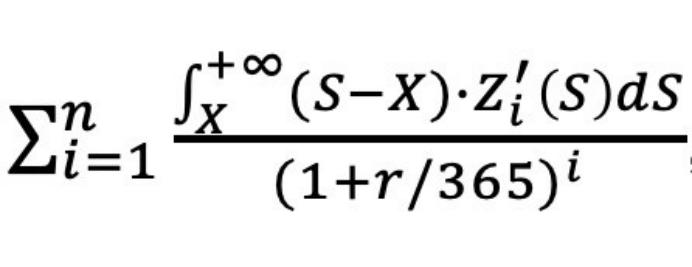
Python模拟
我们用Python模拟了这种认购期权的定价方式:假设现价为100美元,无风险利率为6%,波动率为26%,我们研究这种认购期权价格C和到期天数n之间的关系。
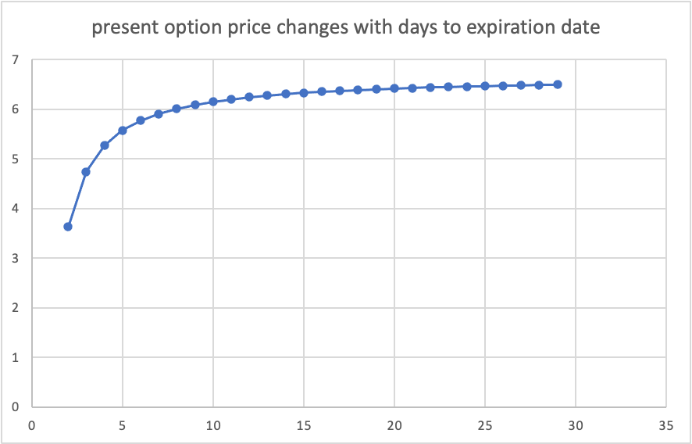
这种情况很符合日常感觉,如果到期天数长,风险增加,价格超过行权价的可能性也增加了。因此认购期权就贵了,但是增长幅度变慢了,如果到期天数无限大,价格应该会收敛到一个定值。
永续时间转换期权的定价方式(以认购期权为例)
在上式中令n趋近于无穷大,我们可以得到这种期权的定价模型为:
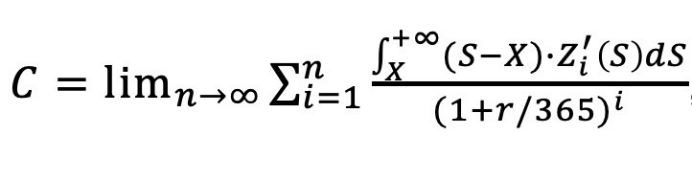
原文链接:https://medium.com/@Vincent.R.Jaipul/perpetual-timer-option-pricing-8bd9f4139e79



