德国亚琛工业大学提出DualConvMesh-Net更好处理3D网格数据
将门创投对于网格形式的3D数据学习一直以来是三维深度学习研究的重点,网格的复杂性和不规则性使得通常的卷积网络无法有效的应用。为此来自德国亚琛工业大学的研究人员们提出了一种集成测地线卷积和欧几里得卷积的层级卷积模型DualConvMesh-Net,用于处理三维几何数据,其中定义在网格表面的测地线卷积可以将作用于给定网格的局域表面,更加注重对于不同目标的编码与分离;而定义在邻域的欧几里得卷积则独立于表面结构,着重于分析区域内点之间的相互关系、编码邻近目标间的相关性,而不注重目标的独立性。
通过有效结合欧几里得卷积和测地线卷积,基于层级结构实现多尺度多分辨率的网格分析,最终大幅度提升了三维语义分割任务的性能,并在多个数据集上取得了优异的结果。

向三维几何进军的深度学习
随着深度学习在图像领域取得了令人瞩目的成就,研究人员们也逐渐开始将深度学习方法特别是卷积神经网络从规则、离散的音频、图像和体素领域,向非规则的几何数据上进行应用。典型的几何数据包括图结构、点云和3D网格等,目前针对这一领域的研究基于数据表示的不同主要分为两大方向:3D场景理解和3D形状分析。
其中3D场景理解的主要任务包括语义分割、实例分割、部件分割等等,所面对的通常是点云数据。人们常常将原始点云转换到规则的离散三维栅格中,以便标准的3D卷积处理。而直接处理点云显然是一种更为便捷的方法,但最大的挑战则来自于如何将卷积作用于非规则的点集上。这种方式通常将卷积核作用于利用球或者K最邻近等欧几里得方法得到的邻域点集中。这种基于欧式距离的欧式卷积关注与点与点之间的相互关系,还对表面形变非常敏感。
与三维场景理解不同的是,三维形状分析主要集中于形状关系、形状描述和检索方面,主要关注以网格或者图形式所编码的表面信息。这种情况下,卷积核通常定义在网格或者图的局域片层上,通过测地线距离来进行定位和联系(可以理解为沿着物体表面连接两个节点见最短的边)。这种方式的卷积被称为测地线卷积,其最主要的特性是对于曲面形变具有不变形的特点,因此非常适合与独立个体的描述与辨别。
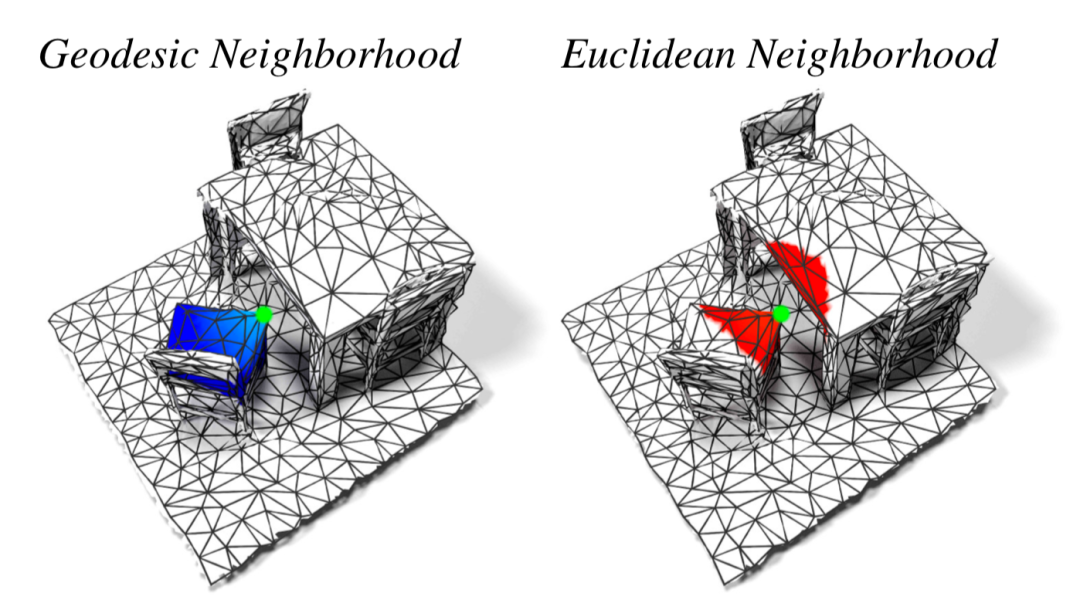
上图彩色梯度显示了两种不同卷积的特点,可以看到测地线距离可以有效分离出独立的个体,它专注于沿着表面进行学习;而欧式距离则更多地专注于空间相关性,可以衔接起小部分的缺失,以便学习到更多的上下文信息,补全缺失部分。
在这篇文章中,研究人员探索了上述的两种卷积在三维网格语义分割任务中的应用。目前绝大多数方法都基于欧式卷积,很少有利用测地线方法来进行的研究。欧式卷积主要专注于上下文和邻域信息的学习,而测地线距离则主要针对特定目标,沿着其表面进行形状学习。这两种方法各有优劣,那么如何将他们的优势结合起来提升模型性能呢?
为了解决这一问题,建立结合两种卷积的综合架构,研究人员提出了DualConvMesh-Net,在网格数据下利用两种卷积对几何结构进行综合学习与处理。为了在不同尺度上对欧式特征和测地线特征进行学习,不仅构建了层级网络架构,同时提出网格池化算法来在各个层级上简化并保留重要的网格结构。下面就详细地了解模型如何融合不同卷积方法并对网格进行简化和学习的。
DualConvMesh-Net
本文提出的DualConvMesh-Net(DCM-Nets)是一类层级深度网络架构,它结合了测地线图卷积在3D表面网格上的优势和欧几里得图卷积在空间域中3D顶点上的优势。网络的输入是包含了顶点信息的网格、输入则是包含顶点特征的网格,可以有效用于稠密预测任务。网络通过模块化的形式构建,具有容易集成与测评的优势。
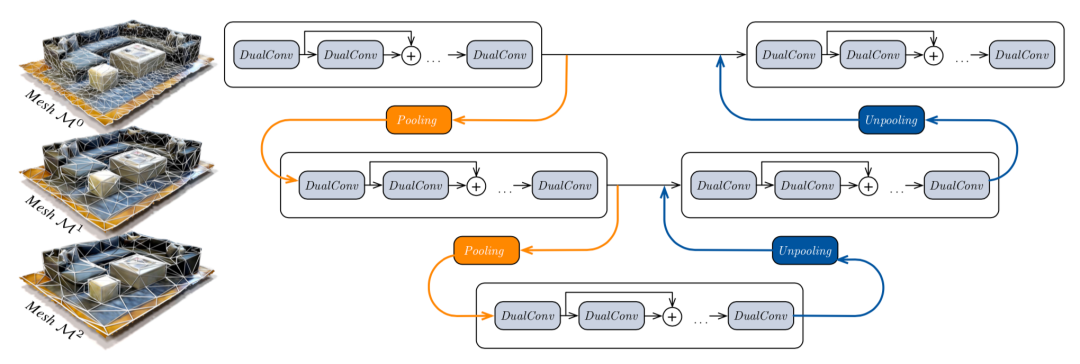
本文提出的主体网络架构如下图所示,在编码器解码器架构的基础上添加了衔接的残差结构,便于训练收敛。可以看到网络由多个层级组成,每个层级中包含了多个叠加的DualConv结构。在DualConv结构中,测地线卷积和欧式卷积并行作用,并将得到的特征图进行衔接输出。而针对不同尺度的网格,则需要利用池化算法来对网格进行简化。
针对欧几里得图卷积和测地线图卷积,针对某个尺度的网格来说其顶点(Vertex)为欧式空间中的点集,而其边则分为了基于knn或者一定邻域半径内得到的欧几里得形式的边,以及基于网格上的面而得到的测地线边(Edge).而最终卷积作用于与顶点对应的特征xi上,输出yi为顶点vi的对应特征:
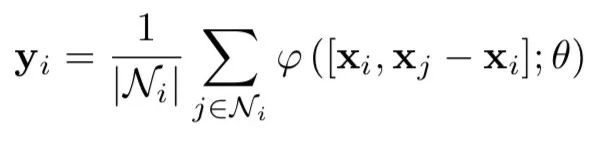
其中N表示顶点附近的邻域,φ为训练的非线性映射函数。值得注意的是,卷积核参数θ的数量与核的大小无关,同时归一化的分母提高了卷积对于不同邻域数量的鲁棒性。针对网络最开始的卷积层,定义了仅仅依赖边缘信息具有不变形的卷积操作,仅仅输入xj-xi,而去除了包含绝对位置的初始特征xi。这样的改变是的模型可以在场景的片层上训练,但同时可以在完整的结构上进行测评,不仅为每个顶点带来更广的上下文区域,同时也减少了运行时间。此外对于初始欧几里得与侧地线空间邻域的复用则使得更深的图卷积成为可能,同时也减少了运行的内存需求提高的计算速度。
1 2 3 下一页>

