人工智能之TD Learning算法

    人工智能机器学习有关算法内容，请参见公众号“科技优化生活”之前相关文章。人工智能之机器学习主要有三大类：1）分类；2）回归；3）聚类。今天我们重点探讨一下TD Learning算法。 ＾＿＾
    TD Learning时序差分学习结合了动态规划DP和蒙特卡洛MC（请参见人工智能（31））方法，且兼具两种算法的优点，是强化学习的核心思想。
    虽然蒙特卡罗MC方法仅在最终结果已知时才调整其估计值，但TD Learning时序差分学习调整预测以匹配后，更准确地预测最终结果之前的未来预测。
    
    TD Learning算法概念：
    TD Learning（Temporal－Difference Learning） 时序差分学习指的是一类无模型的强化学习方法，它是从当前价值函数估计的自举过程中学习的。这些方法从环境中取样，如蒙特卡洛方法，并基于当前估计执行更新，如动态规划方法。
    TD Learning算法本质：
    TD Learning（Temporal－DifferenceLearning）时序差分学习结合了动态规划和蒙特卡洛方法，是强化学习的核心思想。
    时序差分不好理解。改为当时差分学习比较形象一些，表示通过当前的差分数据来学习。
    蒙特卡洛MC方法是模拟（或者经历）一段序列或情节，在序列或情节结束后，根据序列或情节上各个状态的价值，来估计状态价值。TD Learning时序差分学习是模拟（或者经历）一段序列或情节，每行动一步（或者几步），根据新状态的价值，然后估计执行前的状态价值。可以认为蒙特卡洛MC方法是最大步数的TD Learning时序差分学习。
    TD Learning算法描述：
    如果可以计算出策略价值（π状态价值vπ（s），或者行动价值qπ（s，a）），就可以优化策略。
    在蒙特卡洛方法中，计算策略的价值，需要完成一个情节，通过情节的目标价值Gt来计算状态的价值。其公式：
    MC公式：
    V（St）←V（St）＋αδt
    δt＝［Gt？V（St）］
    这里：
    δt – MC误差
    α – MC学习步长
    TD Learning公式：
    V（St）←V（St）＋αδt
    δt＝［Rt＋1＋γV（St＋1）？V（St）］
    这里：
    δt – TD Learning误差
    α – TD Learning步长
    γ – TD Learning报酬贴现率
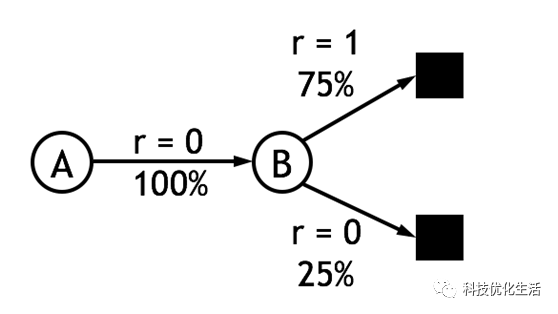
    TD Learning时间差分方法的目标为Rt＋1＋γ V（St＋1），若V（St＋1） 采用真实值，则TD Learning时间差分方法估计也是无偏估计，然而在试验中V（St＋1）  用的也是估计值，因此TD Learning时间差分方法属于有偏估计。然而，跟蒙特卡罗MC方法相比，TD Learning时间差分方法只用到了一步随机状态和动作，因此TD Learning时间差分方法目标的随机性比蒙特卡罗MC方法中的Gt 要小，因此其方差也比蒙特卡罗MC方法的方差小。
    
    TD Learning分类：
    1）策略状态价值vπ的时序差分学习方法（单步多步）
    2）策略行动价值qπ的on－policy时序差分学习方法： Sarsa（单步多步）
    3）策略行动价值qπ的off－policy时序差分学习方法： Q－learning（单步），Double Q－learning（单步）
    4）策略行动价值qπ的off－policy时序差分学习方法（带importance sampling）： Sarsa（多步）
    5）策略行动价值qπ的off－policy时序差分学习方法（不带importance sampling）： Tree Backup Algorithm（多步）
    6）策略行动价值qπ的off－policy时序差分学习方法： Q（σ）（多步）
    TD Learning算法流程：
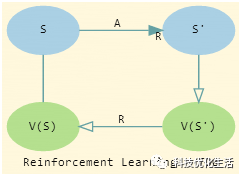
    1）单步TD Learning时序差分学习方法：
    InitializeV（s） arbitrarily ？s∈S＋
    Repeat（for each episode）：
    ？Initialize S
    ？Repeat （for each step of episode）：
    ？？ A←actiongiven by π for S
    ？？Take action A， observe R，S′
    ？？V（S）←V（S）＋α［R＋γV（S′）？V（S）］
    ？？ S←S′
    ？Until S is terminal
    
    2）多步TD Learning时序差分学习方法：
    Input：the policy π to be evaluated
    InitializeV（s） arbitrarily ？s∈S
    Parameters：step size α∈（0，1］， a positive integer n
    Allstore and access operations （for St and Rt） can take their index mod n
    Repeat（for each episode）：
    ？Initialize and store S0≠terminal
    ？ T←∞
    ？ Fort＝0，1，2，？：
    ？？ Ift＜Tt＜T， then：
    ？？？Take an action according to π（ ˙｜St）
    ？？？Observe and store the next reward as Rt＋1 and the next state as St＋1
    ？？？If St＋1 is terminal， then T←t＋1
    ？？ τ←t？n＋1（τ is the time whose state＇s estimate is being updated）
    ？？ Ifτ≥0τ≥0：
    ？？？ G←∑min（τ＋n，T）i＝τ＋1γi？τ？1Ri
    ？？？if τ＋n≤Tτ＋n≤T then： G←G＋γnV（Sτ＋n）（G（n）τ）
    ？？？V（Sτ）←V（Sτ）＋α［G？V（Sτ）］
    ？Until τ＝T？1
    
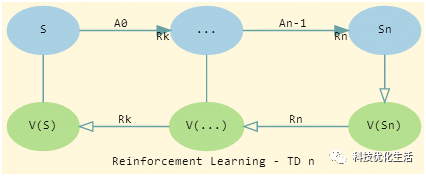
    注意：V（S0）是由V（S0），V（S1），…，V（Sn）计算所得；V（S1）是由V（S1），V（S1），…，V（Sn＋1）计算所得。
    TD Learning理论基础：
    TD Learning理论基础如下：
    1）蒙特卡罗方法
    2）动态规划
    3）信号系统
    TD Learning算法优点：
    1）不需要环境的模型；
    2）可以采用在线的、完全增量式的实现方式；
    3）不需等到最终的真实结果；
    4）不局限于episode task；
    5）可以用于连续任务；
    6）可以保证收敛到 vπ，收敛速度较快。
    TD Learning算法缺点：
    1）    对初始值比较敏感；
    2）    并非总是用函数逼近。
    TD Learning算法应用：
    从应用角度看，TD Learning应用领域与应用前景都是非常广阔的，目前主要应用于动态系统、机器人控制及其他需要进行系统控制的领域。
    结语：
    TD Learning是结合了动态规划DP和蒙特卡洛MC方法，并兼具两种算法的优点，是强化学习的中心。TD Learning不需要环境的动态模型，直接从经验经历中学习；也不需要等到最终的结果才更新模型，它可以基于其他估计值来更新估计值。输入数据可以刺激模型并且使模型做出反应。反馈不仅从监督学习的学习过程中得到，还从环境中的奖励或惩罚中得到。TD Learning算法已经被广泛应用于动态系统、机器人控制及其他需要进行系统控制的领域。
    －－－－－－以往文章推荐－－－－－－
    机器学习
    深度学习
    人工神经网络
    决策树
    随机森林
    强化学习
    迁移学习
    遗传算法
    朴素贝叶斯
    支持向量机
    蒙特卡罗方法
    马尔科夫模型
    Hopfield神经网络
    回归模型
    K邻近算法
    卷积神经网络
    受限玻尔兹曼机
    循环神经网络
    长短时记忆神经网络
    Adaboost算法
    ID3算法
    CART算法
    K－Means算法
    Apriori算法
    PCA算法
    ICA算法