人工智能之回归模型（RM）

    前言：人工智能机器学习有关算法内容，请参见公众号之前相关文章。人工智能之机器学习主要有三大类：1）分类；2）回归；3）聚类。今天我们重点探讨一下回归模型（RM）。 
    
    回归不是单一的有监督学习技术，而是许多技术所属的整个类别。回归的目的是预测数值型的目标值，如预测商品价格、未来几天的PM2．5等。最直接的办法是依据输入写出一个目标值的计算公式，该公式就是所谓的回归方程（regressionequation）。求回归方程中的回归系数的过程就是回归。回归是对真实值的一种逼近预测。回归是统计学中最有力的算法之一。
    
    回归概念：
    回归是一个数学术语，指研究一组随机变量（Y1，Y2 ，…，Yi）和另一组（X1，X2，…，Xk）变量之间关系的统计分析方法，又称多重回归分析。其中， X1、X2，…，Xk是自变量，Y1，Y2，…，Yi是因变量。
    回归模型：
    回归模型（Regression Model）对统计关系进行定量描述的一种数学模型。它是一种预测性的建模技术，研究的是因变量（目标）和自变量（预测器）之间的关系。这种技术通常用于预测分析，时间序列模型以及发现变量之间的因果关系。
    回归分析：
    回归模型重要的基础或者方法就是回归分析。回归分析是研究一个变量（被解释变量）关于另一个（些）变量（解释变量）的具体依赖关系的计算方法和理论，是建模和分析数据的重要工具。回归分析是用已知样本对未知公式参数的估计，给出一个点集D，用一个函数去拟合这个点集，并且使得点集与拟合函数间的误差最小。
    回归分类：
    在统计学中，回归分析（regression analysis）指的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。回归分析按照涉及的变量多少，分为一元回归和多元回归分析；按照因变量的多少，可分为简单回归分析和多重回归分析；按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析。
    常见的回归种类有：线性回归、曲线回归、逻辑回归等。
    线性回归：
    如果拟合函数为参数未知的线性函数，即因变量和自变量为线性关系时，则称为线性回归。
    
    通过大量训练，得到一个与数据拟合效果最好的模型，可利用一些算法（比如最小二乘法、梯度下降法等）和工具（SPSS）来更快更好的训练出适用的线性回归模型。实质是求解出每个特征自变量的权值θ。
    在训练过程中，特征选择，拟合优化等都需要考虑。
    最终目标是确定每个权值（参数）θ或者通过算法逼近真实的权值（参数）θ。
    需要注意的是，线性回归不是指样本的线性，样本可以是非线性的，而是指对参数θ的线性。
    线性回归问题：可能会出现欠拟合、非满秩矩阵问题等。
    
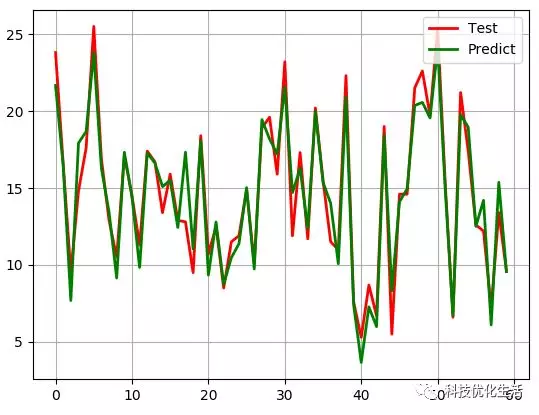
    解决方法：解决欠拟合问题，可采用局部加权线性回归LWLR（Locally Weighted Linear Regression）。解决非满秩矩阵问题，可使用岭回归RR（ridge regression）、Lasso法、前向逐步回归等。
    算法优点：
    1）最可解释的机器学习算法之一，理解与解释都十分直观；
    2）易于使用，因为需要最小的调谐；
    3）运行快，效率高；
    4）最广泛使用的机器学习技术。
    非线性回归：
    如果拟合函数为参数未知的非线性函数，则称为非线性或曲线回归。非线性函数的求解一般可分为将非线性变换成线性和不能变换成线性两大类。
    1） 变换成线性：处理非线性回归的基本方法。通过变量变换，将非线性回归化为线性回归，然后用线性回归方法处理。一般采用线性迭代法、分段回归法、迭代最小二乘法等。
    2）不能变换成线性：基于回归问题的最小二乘法，在求误差平方和最小的极值问题上，应用了最优化方法中对无约束极值问题的一种数学解法——单纯形法。该算法比较简单，收敛效果和收敛速度都比较理想。
    
    常见的非线性回归模型：1）双曲线模型；2）幂函数模型；3）指数函数模型；4）对数函数模型；5）多项式模型。
    
    
    1  2  下一页>