科普 | 天冷了，干了这碗“零知识证明”鸡汤

    前言：从一锅鸡汤说起
    当读者刚开始接触零知识证明的概念时，面临第一关就是如何搞懂突如其来的大量名词，比如离散对数问题、双线性对（Pairing）还有Groth16、PLONK、RedShift等。不妨我们借用“烹饪”这个生活场景来类比其中的层次关系。
    如果把“密码学”比做“烹饪”，那么上个系列中对双线性对的学习就类似于学习炖汤前先简单了解的高压锅的工作原理，而zkSNARK则相当于在说明如何用高压锅炖出美味鸡汤。
    

• 由此可见，双线性对是类似基础工具的角色：就像高压锅既可以炖鸡汤也可以炖排骨汤，双线性对既可以用于零知识证明也可以用于构造签名（例如BLS签名）等密码学算法。
• 而Groth16、PLONK、RedShift等，它们同属于zkSNARK（非交互式简洁零知识论证），属于同一层次，如果沿用上述类比，那大概就是对应用高压锅做汤的风味选择了。

    Groth16算法是Jens Groth提出的一种zkSNARK算法[1]，相关论文不仅对已有算法进行改进，而且讨论了基于配对的非交互式零知识论证的证明大小问题。Groth16因其精简的证明大小和高效的验证效率，在ZCash等项目中多有应用，是最经典的零知识证明算法之一。
    上一个系列中我们完整介绍了零知识证明中用到的椭圆曲线和双线性配对相关的基础知识。本系列通过动手算的方式，以Groth16算法为例，循序渐进地介绍zkSNARK的基本原理。
    本篇是“动手算Groth16”的上篇，主要介绍如何从程序转化为电路和描述算数电路的一种约束系统R1CS。下篇会介绍如何从R1CS转化为多项式相关的约束问题，并且详细给出完整的Groth16从头到尾的手算步骤。
    程序与电路
    初始接触通用零知识证明算法时，读者可能最容易感到疑惑的地方就是各种资料中频繁提到的“电路”一词。这里的“电路”是指什么？它又如何等价地对同一个问题进行描述呢？回答这些问题最简单的方式就是使用具体的一个算法例子进行说明。比如我们有下面一段程序代码，如何将其转化为等价的电路呢？
    
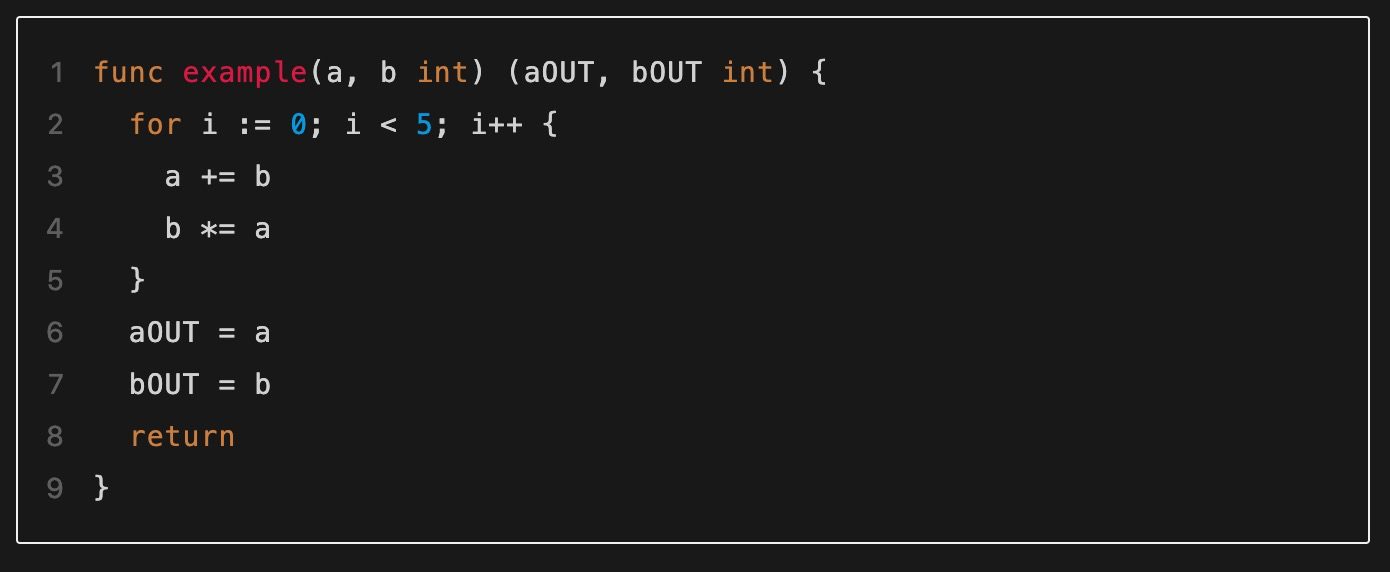
    ▲需要被转化为电路的代码
    这里需要注意到程序中值被存储在变量中，而电路中的值是用电路门之间的连线表示的。这其中有个关键的不同是：变量的值是会随着时间变化的，而电路中连线的值是固定不能改变的。因此首先我们通过引入一些中间量（连线）的方式表示随循环而不断变化的各阶段的变量值，中间量命名为tmp1,tmp2...这样的形式：
    
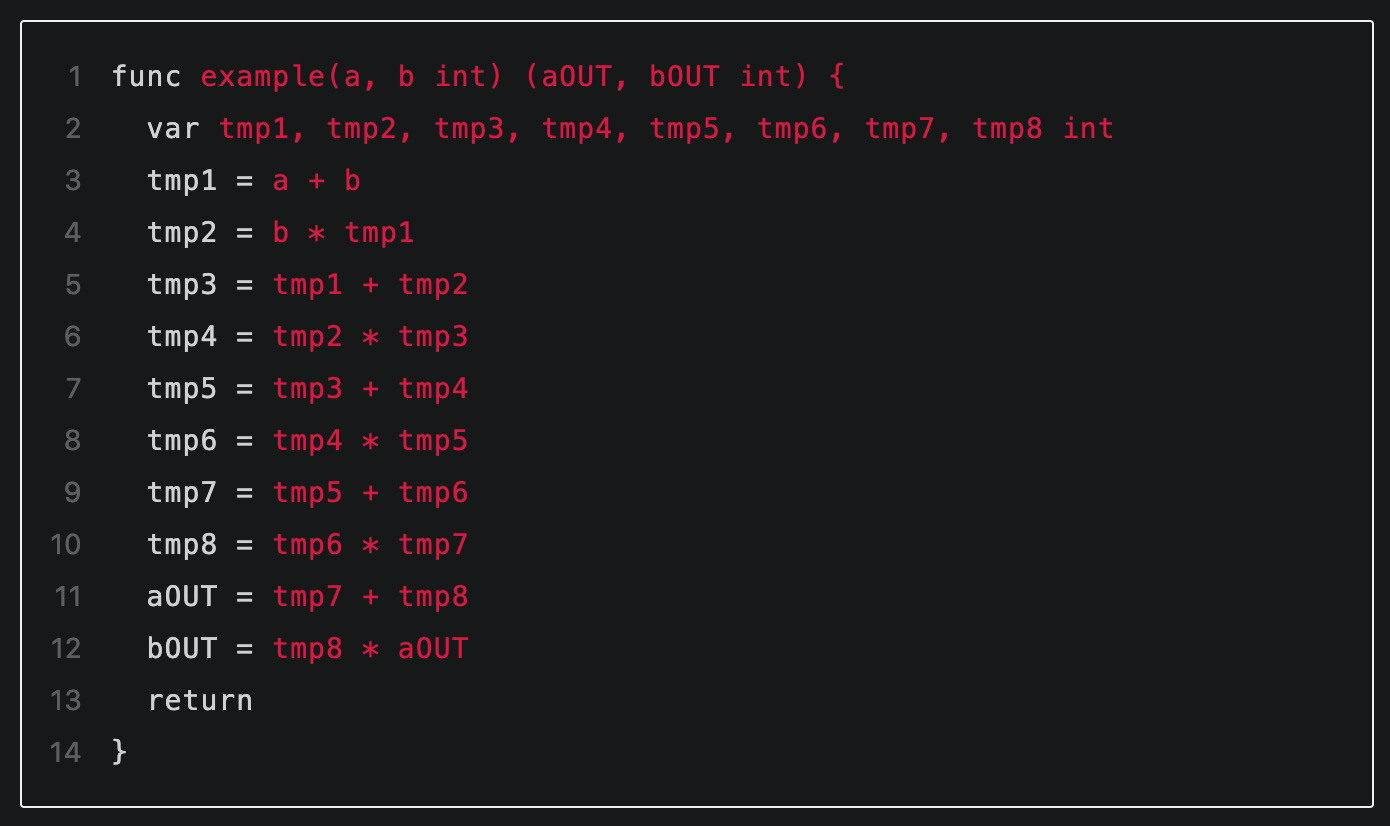
    ▲引入辅助的中间量
    最后我们可以转化为只有加法门和乘法门的算数电路：
    
    ▲电路示意图
    这里除去输入和输出外，其他的圆圈代表了电路中的门：可以是乘法门或者加法门。而门和门之间的连线对应了程序中的中间变量在某个时刻的值。
    如果站在更高的角度思考，其实可以发现有很多结构都能实现“运算”功能，比如说神经元组成的人脑，比如冯·诺伊曼结构的计算机，甚至更早的机械计算器和当今的人工神经网络。算数电路也是这样的一种能够完成一定运算的结构，而且基于这种结构我们能够完成对计算输入和过程的“零知识证明”。因此通用零知识证明算法普遍引入了“电路”这个运算结构并且会研究，如何更好的将高级语言描述的问题转化为等价的算法电路。
    上面例子中约束较多，会给后续的“动手算”产生较多的计算量压力，因此在下文中我们以一个新的例子重新展示这个转化的过程。本系列后续文章都会以这个新的例子为主线进行叙述，从而真实展示证明和验证的具体计算过程。新例子的程序代码如下：
    
    这里涉及到4个连线（两个输入a，b和两个输出c，d）以及两个等式关系。这两个等式关系用更规范的方式重写一下可以帮助读者看地更清晰：
    
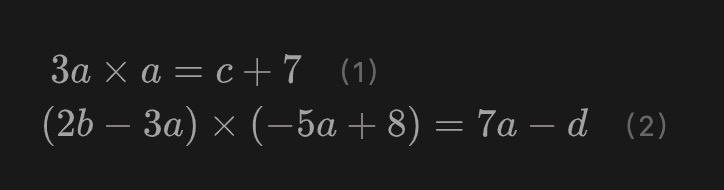
    观察这两个式子的特点，可以发现两个等式关系其实都可以写作A×B=C的形式，其中A、B和C都是变量的“加权组合”。这并非巧合，而是我们有意为之。通过这种形式我们避免了对加法门的约束产生额外开销，而是在对乘法门进行约束的同时零开销的对加法关系进行约束，这是groth16的特点之一。在Groth16算法中，加法门和乘法门的地位并不是等价的，我们更关心乘法门。
    下面对a,b,c,d四个变量赋予编号，以便下一步的处理,按照groth16的习惯我们将输出排列在输入之前：
    
    可以看到除了连线a、b、c和d，还有一个特殊的连线“1”，“1”其实可以看作是一个特殊的公共输入，他的存在让我们在算法中能更容易地处理常量。“1”的值总是1。
    从电路到R1CS
    本部分之前先回顾一下向量的内积概念，向量的内积是从两个同维向量得到一个标量的运算，其几何意义对应了“投影”这个概念。比方说两个二维向量的乘法（内积）：
    （2，3）·（4，1）= 2×4+3×1 = 11
    

• 回过头看刚才的结果，因为A×B=C这个形式的存在，我们其实能够进一步的对这些等式关系进行抽象。抽象的目的是为了方便编程处理和下一步的讨论。
• 以式子(2)为例，我们其实可以认为他是如下的形式：

    
    根据上面介绍的向量内积，可以发现这里的A，B，C其实都是向量内积的形式:
    
    这里的s其实就是全部的连线的值，如果证明者P是真的计算过这个电路的，则P能够获知s的值，否则P无法得知s的值。我们将这个s称为witness。因此通过上面的向量a, b, c我们就能够对s进行一定的约束，即s应该满足：
    
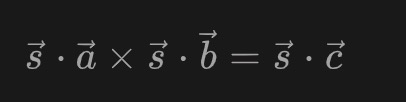
    这就构成了一个一阶约束（R1C, Rank-1 Constraint）,这样的一个约束对应了电路中的一个乘法门。如果我们将所有的约束联立起来，就得到一个一阶约束系统（R1CS，Rank-1 Constraints?System）。通过R1CS我们可以更方便的形式化描述一个零知识证明问题，从而为我们后续解决该问题提供了条件。
    下篇我们会介绍如何将R1CS描述转换为多项式描述，并且通过完整的计算过程展示groth16算法的相关内容，敬请关注。