人工智能之Hopfield神经网络(HNN)
AI优化生活神经网络在1980年代复兴归功于物理学家约翰·霍普菲尔德(Hopfield)。1982年,霍普菲尔德提出了一种新的神经网络,可以解决一大类模式识别问题,还可以给出一类组合优化问题的近似解。这种神经网络模型后被称为Hopfield神经网络。

Hopfield神经网络是一种循环神经网络[请参见公众号“科技优化生活”之人工智能(23)],由约翰·霍普菲尔德发明,他将物理学的相关思想(动力学)引入到神经网络的构造中,从而形成了Hopfield神经网络。贝尔实验室在1987年成功在Hopfield神经网络的基础上研制出了神经网络芯片。
Hopfield神经网络是一种递归神经网络,从输出到输入均有反馈连接,每一个神经元跟所有其他神经元相互连接,又称为全互联网络。
Hopfield神经网络概述:
Hopfield神经网络HNN(Hopfiled Neural Network)是一种结合存储系统和二元系统的神经网络。它保证了向局部极小的收敛,但收敛到错误的局部极小值(local minimum),而非全局极小(global minimum)的情况也可能发生。Hopfield神经网络也提供了模拟人类记忆的模型。
Hopfield神经网络是反馈神经网络,其输出端又会反馈到其输入端,在输入的激励下,其输出会产生不断的状态变化,这个反馈过程会一直反复进行。假如Hopfield神经网络是一个收敛的稳定网络,则这个反馈与迭代的计算过程所产生的变化越来越小,一旦达到了稳定的平衡状态,Hopfield网络就会输出一个稳定的恒值。
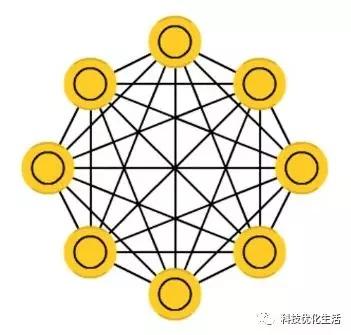
对于一个Hopfield神经网络来说,关键在于确定它在稳定条件下的权系数。
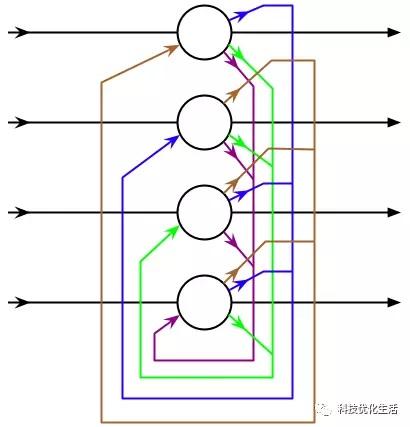
Hopfield神经网络分为两种:1)离散型Hopfield神经网络;2)连续型Hopfield神经网络。
离散型Hopfield神经网络:
Hopfield最早提出的网络是二值神经网络,各神经元的激励函数为阶跃函数或双极值函数,神经元的输入、输出只取{0,1}或者{ -1,1},所以也称为离散型Hopfield神经网络DHNN(Discrete Hopfiled Neural Network)。在DHNN中,所采用的神经元是二值神经元;因此,所输出的离散值1和0或者1和-1分别表示神经元处于激活状态和抑制状态。
离散Hopfield神经网络DHNN是一个单层网络,有n个神经元节点,每个神经元的输出均接到其它神经元的输入。各节点没有自反馈。每个节点都可处于一种可能的状态(1或-1),即当该神经元所受的刺激超过其阀值时,神经元就处于一种状态(比如1),否则神经元就始终处于另一状态(比如-1)。
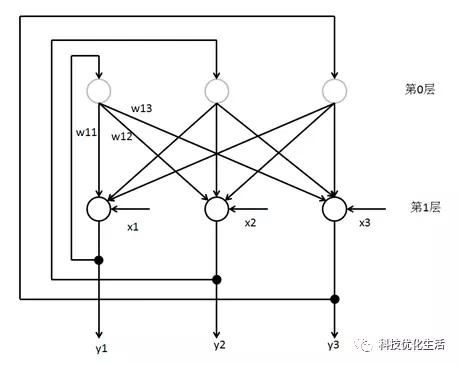
DHNN有两种工作方式:
1)串行(异步)方式:在时刻t时,只有某一个神经元j的状态发生变化,而其他n-1个神经元的状态不变,称为串行工作方式。并且有:
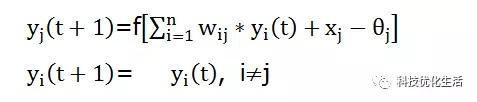
2)并行(同步)方式:在任一时刻t,所有的神经元的状态都产生了变化,称为并行工作方式。并且有:
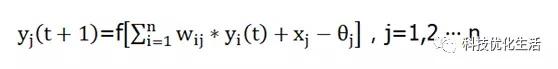
DHNN稳定性:
假设一个DHNN,其状态为Y(t):
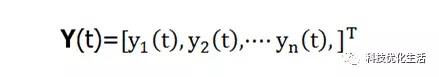
如果对于任何Δt>0,当神经网络从t=0开始,有初始状态Y(0)。经过有限时刻t,有:
Y(t+Δt)=Y(t)
则认为该DHNN网络是稳定的,称其状态为为稳定状态。DHNN网络的稳定状态X就是网络的吸引子(attractor),用于存储记忆信息。串行方式下的稳定性称为串行稳定性;并行方式下的稳定性称为并行稳定性。
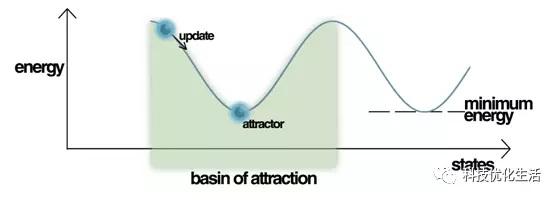
DHNN是一种多输入、含有阈值的二值非线性动态系统。在动态系统中,平衡稳定状态可以理解为系统某种形式的能量函数(energy function)在系统运行过程中,其能量不断减少,最后处于最小值。
DHNN稳定的充分条件:如果DHNN的权系数矩阵W是一个对称矩阵,并且对角线元素为0,则这个网络是稳定的。即在权系数矩阵W中,如果:
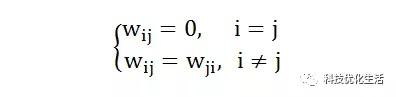
则该DHNN是稳定的。
W是一个对称矩阵仅是充分条件,不是必要条件。
DHNN联想记忆功能:
DHNN一个重要功能是可以用于联想记忆,即联想存储器,这是人类的智能特点之一。

要实现联想记忆,DHNN必须具有两个基本条件:
1) 网络能收敛到稳定的平衡状态,并以其作为样本的记忆信息;
2) 具有回忆能力,能够从某一残缺的信息回忆起所属的完整的记忆信息。
DHNN实现联想记忆过程分为两个阶段:
1)学习记忆阶段: 设计者通过某一设计方法确定一组合适的权值,使DHNN记忆期望的稳定平衡点。
2)联想回忆阶段: DHNN的工作过程。
记忆是分布式的,而联想是动态的。
对于DHNN,由于网络状态是有限的,不可能出现混沌状态。
DHNN局限性:
1)记忆容量的有限性;
2)伪稳定点的联想与记忆;
3)当记忆样本较接近时,网络不能始终回忆出正确的记忆等;
4)DHNN平衡稳定点不可以任意设置,也没有一个通用的方式来事先知道平衡稳定点。
连续型Hopfield神经网络:
连续Hopfield神经网络CHNN(Continuous Hopfield Neural Network)与DHNN在拓扑结构上是一致的。
CHNN稳定性:
CHNN稳定条件要求:
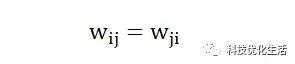
CHNN与DHNN不同之处在于其函数g不是阶跃函数,而是S型的连续函数。一般取:
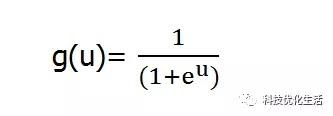
CHNN在时间上是连续的,所以CHNN网络中各个神经元是处于同步方式工作的。
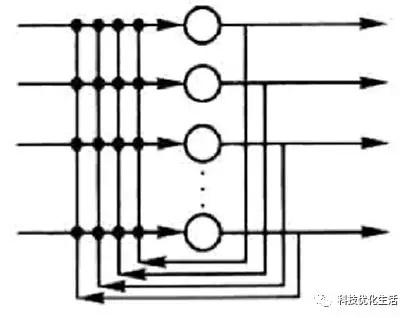
当CHNN网络的神经元传递函数g是连续且有界的(如Sigmoid函数),并且CHNN网络的权值系数矩阵对称,则这个CHNN网络是稳定的。
优化问题:
在实际应用中的系统,如果其优化问题可以用能量函数E(t)作为目标函数,那么CHNN网络和优化问题直接对应。这样,大量优化问题都可以用CHNN网络来求解。这也是Hopfield网络用于神经计算的基本原因。
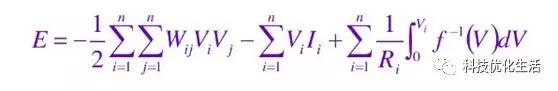
CHNN与DHNN主要区别:
CHNN与DHNN的主要差别在于:CHNN神经元激活函数使用Sigmoid函数,而DHNN神经元激活函数使用了硬极限函数。
Hopfield神经网络应用:
Hopfield神经网络早期应用包括按内容寻址存储器,模数转换及优化组合计算等。具有代表意义的是解决TSP问题,1985年Hopfield和Tank用Hopfield网络求解N=30的TSP问题,从而创建了神经网络优化的新途径。除此之外,Hopfield 神经网络在人工智能之机器学习、联想记忆、模式识别、优化计算、VLSI和光学设备的并行实现等方面有着广泛应用。

结语:
Hopfield神经网络(HNN)是一种具有循环、递归特性,结合存储和二元系统的神经网络。由约翰·霍普菲尔德在1982年发明。对于一个Hopfield神经网络来说,关键在于确定它在稳定条件下的权系数。Hopfield神经网络分为离散型和连续型两种,主要差别在于激活函数的不同。Hopfield神经网络(HNN)提供了模拟人类记忆的模型。它在人工智能之机器学习、联想记忆、模式识别、优化计算、VLSI和光学设备的并行实现等方面有着广泛应用。
原创 张志荣

