CPU 中的加法器,为什么可以连同符号位一起运算?
道哥分享一、前言
计算机最喜欢的数字就是 0 和 1,在 CPU 的世界中,它只认识这两个数字,即使是强大的操作系统,也都是由 0 和 1 组成的。
作为一名软件开发者,入门学习的内容可能就是认识这 2 个既简单、又强大的数字。但是大部分人,对于二进制、二进制计算、原码、反码以及补码的认识,仍处于机械的强制记忆阶段。尤其是对一些编码和计算,仍然处于模糊的认识阶段,例如:
CPU 是如何表示负数的?
为什么补码可以用来表示负数?
一个 8 位的二进制数,最小值为什么是 -128,而不是 -127?
CPU 中的加法器,为什么可以连同符号位一起运算?
这篇文章我们就来聊聊这个最最基础的内容,帮助你来理解二进制计算的相关内容,看完这篇文章之后,不仅知其然,更能知其所以然!
PS: 这里有点高调了,最终的所以然部分,应该涉及到数学证明这一层次了,本文并不会涉及到求证过程。
二、从十进制到二进制
1. 十进制
作为数学计算能力强大的中国,10 以内的加减法,应该是在幼儿园阶段就完成了。如果你不属于这个范围,说明你上的是假幼儿园。
我们来快速复习一下关于十进制运算的一些基本知识:
每一个数位上包括的数字为 0 到 9;
每一个数位上的数,是它右侧数位的 10 倍;
两个数相加时,相同数位上的数相加之和如果大于等于 10,就向前进 1 位,即:满十进一;
具体来看就是:
从右数第一个位数(个位)上的数字代表多少个 1;
从右数第二个位数(十位)上的数字代表多少个 10;
从右数第三个位数(百位)上的数字代表多少个 100;
从右数第四个位数(千位)上的数字代表多少个 1000;
十进制的数,可以使用后缀字母 D 来表示,也可以省略。例如:十进制的 1234 这个数字,个位上的数是 4, 十位上的数是 3, 百位上的数是 2,千位上的数是 1(一般是从最右侧的个位说起),每一个数位上的数比它右侧大十倍。如下图:
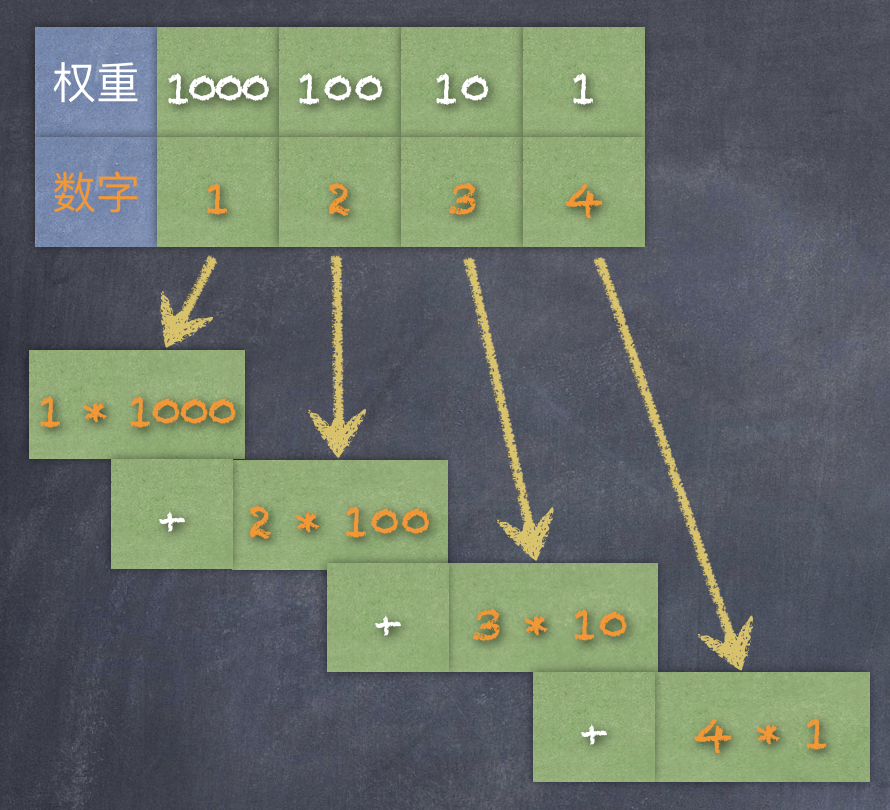
十进制数据,也称作基于十的表示法。
2. 二进制
那么对于二进制呢?直接套用上面十进制的概念,然后把 10 换成 2 即可(目前先忽略符号位):
每一个数位上包括的数字为 0 和 1;
每一个数位上的数,是它右侧数位的 2 倍;
两个数相加时,相同数位上的数相加之和如果大于等于 2,就向前进 1 位,即:满二进一;
具体来看就是:
从右数第一个位数上的数字代表多少个 1;
从右数第二个位数上的数字代表多少个 2;
从右数第三个位数上的数字代表多少个 4;
从右数第四个位数上的数字代表多少个 8;
记住几个重点:二进制数中只包含 0 和 1 两个数字,在相加时满二进一。
在十进制中,每一个数位我们给它进行了专门的命名(个位、十位、百位...),但是二进制没有类似的命名。
二进制的数,使用后缀字母 B 来表示,例如:二进制的 1111B 这个数字,用图来表示权重如下:
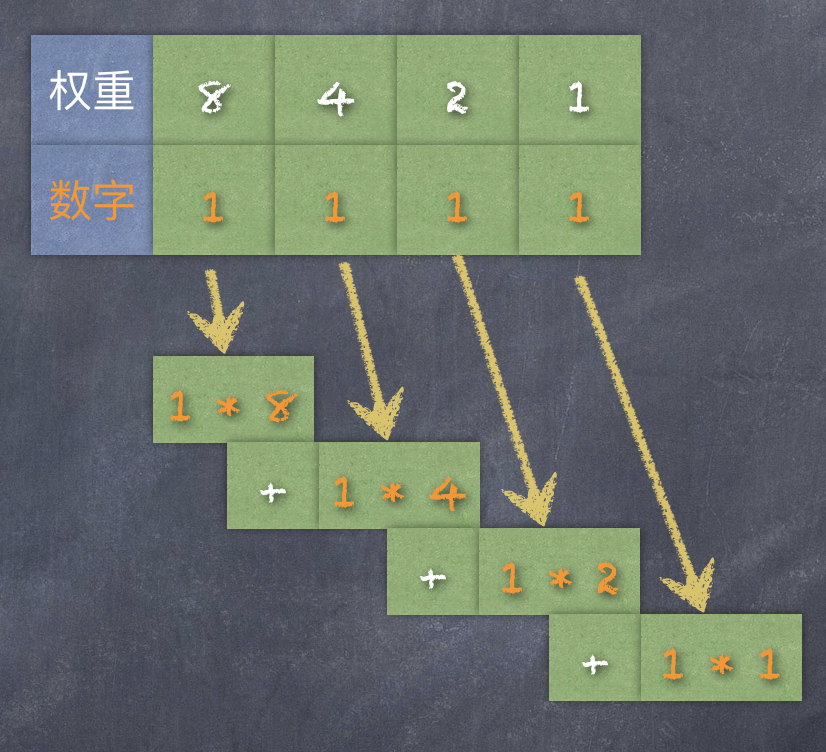
换算成十进制数就是 15(1 * 8 + 1 * 4 + 1 * 2 + 1 * 1 = 15)。
在二进制中,每一位称为一个比特(bit),如果用 8 个 bit 来表示一个二进制数,最小值是 0000_00000,最大值是 1111_1111;
如果用 16 个 bit 来表示一个二进制数,最小值是 0000_0000_0000_0000,最大值是 1111_1111_1111_1111。(为了便于观察,每 4 个 bit 之间,加上了分隔符)
在早期的计算机中,8 位的处理器很常见,于是就给它一个专门的名字:字节(Byte)。16 位的二进制数就是 2 个字节,也称作:字(Word)。
1 2 3 4 下一页>

