人工智能之Q Learning算法

    人工智能机器学习有关算法内容，请参见公众号“科技优化生活”之前相关文章。人工智能之机器学习主要有三大类：1）分类；2）回归；3）聚类。今天我们重点探讨一下Q Learning算法。 ＾＿＾
    通过前一篇TD－Learning时序差分（请参见人工智能（48）算法介绍，我们知道，TD－Learning时序差分是结合了动态规划DP和蒙特卡洛MC（请参见人工智能（31））方法，并兼具两种算法的优点，是强化学习的中心。
    
    TD－learning时序差分大概分了6类。其中，策略行动价值qπ的off－policy时序差分学习方法： Q－Learning（单步），Double Q－Learning（单步）。今天重点介绍Q－Learning算法。
    Q Learning算法是由Watkins于1989年在其博士论文中提出，是强化学习发展的里程碑，也是目前应用最为广泛的强化学习算法。
    Q Learning算法概念：
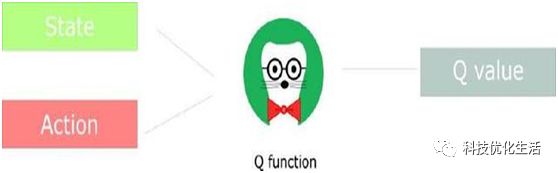
    Q Learning算法是一种off－policy的强化学习算法，一种典型的与模型无关的算法，即其Q表的更新不同于选取动作时所遵循的策略，换句化说，Q表在更新的时候计算了下一个状态的最大价值，但是取那个最大值的时候所对应的行动不依赖于当前策略。
    Q Learning始终是选择最优价值的行动，在实际项目中，Q Learning充满了冒险性，倾向于大胆尝试。
    
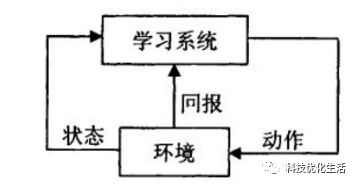
    Q Learning算法下，目标是达到目标状态（Goal State）并获取最高收益，一旦到达目标状态，最终收益保持不变。因此，目标状态又称之为吸收态。
    Q Learning算法下的agent，不知道整体的环境，知道当前状态下可以选择哪些动作。通常，需要构建一个即时奖励矩阵R，用于表示从状态s到下一个状态s’的动作奖励值。由即时奖励矩阵R计算得出指导agent行动的Q矩阵。
    Q矩阵是agent的大脑。
    Q Learning算法本质：
    QLearning属于TD－Learning时序差分学习。同样，该算法结合了动态规划和蒙特卡罗MC算法，模拟（或者经历）一个情节，每行动一步（或多步）后，根据新状态的价值，来估计执行前的状态价值。
    
    下面提到的Q－Learning是单步更新算法。
    Q Learning算法描述：
    Q－learning是一个突破性的算法。
    利用下面公式进行off－policy学习，即用公式来表示Q－Learning中Q表的更新：
    Q（St，At）←Q（St，At）＋α［Rt＋1＋γmax Q（St＋1，a）？Q（St，At）］
    其中：
    St： 当前状态state
    At： 从当前状态下，采取的行动action
    St＋1：本次行动所产生的新一轮state
    At＋1： 次回action
    Rt： 本次行动的奖励reward
    γ为折扣因子，0＜＝ γ＜1，γ＝0表示立即回报，γ趋于1表示将来回报，γ决定时间的远近对回报的影响程度，表示牺牲当前收益，换取长远收益的程度。将累计回报作为评价策略优劣的评估函数。当前的回报值以及以前的回报值都可以得到，但是后续状态的回报很难得到，因此累计回报就难以计算。而Q－learning用Q函数来代替累计回报作为评估函数，正好解决这个问题。
    α为控制收敛的学习率，0＜ α＜1。通过不断的尝试搜索空间，Q值会逐步趋近最佳值Q＊。
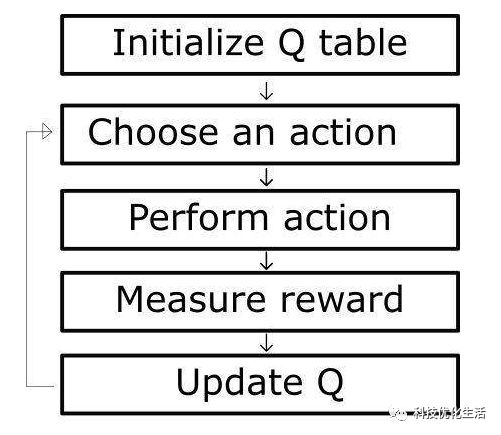
    1）Q－learning单步时序差分学习方法算法描述
    Initialize Q（s，a），？s∈S，a∈A（s） arbitrarily， and Q（terminal， ˙）＝0
    Repeat （for each episode）：
    ？ Initialize S
    ？ Choose A from S using policy derived from Q （e．g． ？？greedy）
    ？ Repeat （for each step of episode）：
    ？？ Take action A， observe R，S′
    ？？ Q（S，A）←Q（S，A）＋α［R＋γmaxa Q（S‘，a）？Q（S，A）］
    ？？ S←S′；
    ？ Until S is terminal
    每个episode是一个training session，且每一轮训练意义就是加强大脑，表现形式是agent的Q矩阵元素更新。当Q习得后，可以用Q矩阵来指引agent的行动。
    Q－learning使用了max，会引起一个最大化偏差（Maximization Bias）问题。
    可以使用Double Q－learning可以消除这个问题。
    
    2）Double Q－learning单步时序差分学习方法算法描述
    Initialize Q1（s，a） and Q2（s，a），？s∈S，a∈A（s） arbitrarily
    Initialize Q1（terminal， ˙）＝Q2（terminal， ˙）＝0
    Repeat （for each episode）：
    ？ Initialize S
    ？ Repeat （for each step of episode）：
    ？？ Choose A from S using policy derived from Q1 and Q2 （e．g． ？？greedy）
    ？？ Take action A， observe R，S′
    ？？ With 0．5 probability：
    ？？？ Q1（S，A）←Q1（S，A）＋α［R＋γQ2（S′，argmax Q1（S′，a））？Q1（S，A）］
    ？？ Else：
    ？？？ Q2（S，A）←Q2（S，A）＋α［R＋γQ1（S′，argmax Q2（S′，a））？Q2（S，A）］
    ？？ S←S′；
    ？ Until S is terminal
    
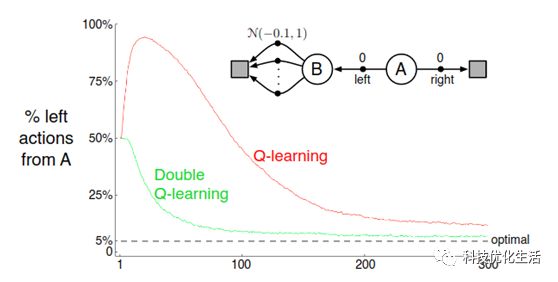
    Double Q Learning算法本质上是将计算Q函数进行延迟，并不是得到一条样本就可以更新价值函数，而是一定的概率才可以更新。由原来的1条样本做到影响决策变为多条（至少两条）样本影响决策。
    Q Learning理论基础：
    QLearning理论基础如下：
    1）蒙特卡罗方法
    2）动态规划
    3）信号系统
    4）随机逼近
    5）优化控制
    Q Learning算法优点：
    1）所需的参数少；
    2）不需要环境的模型；
    3）不局限于episode task；
    4）可以采用离线的实现方式；
    5）可以保证收敛到 qπ。
    Q Learning算法缺点：
    1）    Q－learning使用了max，会引起一个最大化偏差问题；
    2）    可能会出现更新速度慢；
    3）    可能会出现预见能力不强。
    注：使用Double Q－learning可以消除问题1）；使用多步Q －learning可以消除问题2）和3）。
    Q Learning算法应用：
    从应用角度看，Q Learning应用领域与应用前景都是非常广阔的，目前主要应用于动态系统、机器人控制、工厂中学习最优操作工序以及学习棋类对弈等领域。
    结语：
    Q Learning是一种典型的与模型无关的算法，它是由Watkins于1989年在其博士论文中提出，是强化学习发展的里程碑，也是目前应用最为广泛的强化学习算法。Q Learning始终是选择最优价值的行动，在实际项目中，Q Learning充满了冒险性，倾向于大胆尝试，属于TD－Learning时序差分学习。Q Learning算法已经被广泛应用于动态系统、机器人控制、工厂中学习最优操作工序以及学习棋类对弈等领域。